6828. Сортировка хлеба

Майкл работает в пекарне. В конце смены его босс требует отсортировать хлеб в определенном порядке. Она не может пока определиться в каком порядке, хотя как кажется Майклу, каждый день порядок оказывается новым. Майкл проработал уже в пекарне некоторое время и теперь узнал ловкий трюк с его деревянной хлебобулочной лопаткой. Он может принять три хлеба лежащих рядом друг с другом на лопатку и бросить их в воздухе так, что когда они приземлятся, то самый правый переместится в самую левую позицию, а два других хлеба перейдут на одно место вправо. Другими словами, он может вращаться вправо подпоследовательности хлебов длины три.

Еще до конца смены его коллеги разместили хлеб в длинную линию. Майкл хочет отсортировать хлеба, используя трюк с лопаткой. Он может принимать на лопатку любые три последовательных хлеба на линии, вращать их, а затем положить обратно. Иногда даже не имеет значения, сколько раз он использует лопатку – если сортировка линии хлеба по требованию босса просто не представляется возможной.

Вход. Первая строка содержит целое число n (3 ≤ n ≤ 10⁵). Затем следуют две строки: первая строка содержит перестановку чисел от 1 до n, задающих текущий порядок расположений хлебов. Вторая строка содержит перестановку чисел от 1 до n – требуемую босом перестановку хлебов.

Выход. Выведите “Possible”, если Майкл сможет при помощи своей лопатки отсортировать хлеба как требует того его босс. Иначе выведите “Impossible”.

Пример входа 1	Пример выхода 1
4 1 3 4 2 4 3 2 1	Possible
Пример входа 2	Пример выхода 2
6 1 2 3 4 5 6 6 5 4 3 2 1	Impossible

РЕШЕНИЕ

количество инверсий

Анализ алгоритма

Трюк с лопаткой совершает следующую перестановку хлебов:

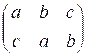
Ее можно получить в результате двух перестановок соседних элементов:

(a, b, c) → (a, c, b) → (c, a, b)

Перестановка соседних элементов изменяет четность перестановки. Следовательно указанная перестановка хлебов сохраняет четность перестановки.

Отсортировать хлеба как требует босс Макйла можно, если только четность перестановок одинакова.

Линейное решение задачи базируется на том, что две перестановки имеют одинаковую четность если только количество циклов, на которые они раскладываются, имеют одинаковую четность.

Пример

В первом примере первая перестановка содержит 2 инверсии, вторая – 6 инверсий. Количество инверсий имеет одну и ту же четность.

Разобьем перестановки на циклы:

· (1, 3, 4, 2) = (1) (3, 4, 2);

· (4, 3, 2, 1) = (4, 1) (3, 2);

Обе перестановки имеют два цикла. Количество циклов в перестановках имеет одну и ту же четность.

Второй пример. Первая перестановка содержит 0 инверсий, вторая – 15 инверсий. Количество инверсий имеет разную четность.

Разобьем перестановки на циклы:

· (1, 2, 3, 4, 5, 6) = (1) (2) (3) (4) (5) (6);

· (6, 5, 4, 3, 2, 1) = (6, 1) (5, 2) (4, 3);

Первая перестановка имеет 6 циклов, вторая – 3 цикла. Количество циклов в перестановках имеет разную четность.

Реализация алгоритма

Вычислим количество инверсий в обоих перестановках за время O(nlog₂n) и сравним их четность.

#include <cstdio>

#include <string>

#include <vector>

#define MAX 100010

using namespace std;

int m[MAX];

int n, i, j;

long long swaps, sw;

void merge(int *a, int bleft, int bright, int cleft, int cright)

{

// a[bleft..bright] -> res[]

// res[0..len-1] a[cleft..cright] are merged into a[bleft..cright]

// we copy only half of array

int i, len = bright - bleft + 1, resCur = 0;

int *res = new int[len];

memcpy(res,a + bleft,len*sizeof(int));

while((resCur < len) && (cleft <= cright))

{

if (res[resCur] <= a[cleft]) a[bleft++] = res[resCur++];

else a[bleft++] = a[cleft++], swaps += len - resCur;

}

while (resCur < len) a[bleft++] = res[resCur++];

delete[] res;

}

void mergeSort(int *a, int left, int right)

{

if (left >= right) return;

int middle = (left + right) / 2;

mergeSort(a,left,middle);

mergeSort(a,middle+1,right);

merge(a, left, middle, middle + 1, right);

}

int main(void)

{

scanf("%d",&n);

for(swaps = i = 0; i < n; i++) scanf("%d",&m[i]);

mergeSort(m, 0, n - 1); sw = swaps % 2;

for(swaps = i = 0; i < n; i++) scanf("%d",&m[i]);

mergeSort(m, 0, n - 1); swaps %= 2;

if (sw == swaps) printf("Possible\n");

else printf("Impossible\n");

return 0;

}

Реализация алгоритма – количество циклов в перестановке

Вычислим количество циклов в каждой перестановке и проверим их на одинаковую четность.

#include <stdio.h>

#define MAX 100010

int i, n, p1, p2, res;

int a[MAX];

void run(int pos)

{

int v;

while(a[pos] != -1)

{

v = a[pos];

a[pos] = -1;

pos = v;

}

}

int parity(int *a)

{

int res, i;

for(res = i = 0; i < n; i++)

if (a[i] != -1)

{

run(i);

res++;

}

return res % 2;

}

int main(void)

{

scanf("%d",&n);

for(i = 0; i < n; i++)

scanf("%d",&a[i]), a[i]--;

p1 = parity(a);

for(i = 0; i < n; i++)

scanf("%d",&a[i]), a[i]--;

p2 = parity(a);

if (p1 == p2) printf("Possible\n");

else printf("Impossible\n");

return 0;

}